LaTeX/Математика
Једна од највећих мотивационих сила Доналда Кнута, када је почео да развија оригинални TeX систем, јесте била била прављење нечега што је омогућавало лако конструкцију математичких формула, али да изгледа професинално кад се одштампа. Чињеница да је успео у својој намери је највероватније разлог због којег је TeX (и касније, LaTeX) постао толико популаран у научном друштву. Куцање математике је једна од највећих LaTeXових врлина. То је, такође, велика тема због постојања толико математичких нотација.
Ако Ваш документ захтева само неколико једноставних математичких формула, обичан LaTeX има већину потребних алата. Ако пишете научни документ који садржи велико број компликованих формула, amsmath package[1] уводи неколико нових команди које су јаче и флексибилније од оних које даје LaTeX. mathtools поправља неке amsmath недостатке и додаје корисна подешавања, симболе, и окружења amsmath-у.[2] За коришћење или једног или другог пакета, откуцајте:
\usepackage{amsmath}
или
\usepackage{mathtools}
у уводу Вашег текста. mathtools пакет учитава amsmath пакет и отуда нема потребе за \usepackage{amsmath} у уводу, ако је mathtools коришћен.
Математичка окружења
[уреди]LaTeX мора да зна да накнадни текст заиста садржи математичке елементе. То је зато што LaTeX куца метаматичке нотације другачије од обичног текста. Стога, посебна окружења су направљена из овог разлога. Могу се поделити на две категорије у зависности од тога како ће бити презентоване:
- text — текстуалне формуле се редно приказују, то јест, унутар тела текста у којем је проглашена, на пример, могу рећи да је a + a = 2a унутар ове реченице.
- displayed — приказује формуле које су одвојене од главног текста.
Како математика захтева посебна окружења, постоје, наравно, одговарајућа имена окружења која можете стандардно користити. За разлику од осталих окружења, међутим, постоје неке згодне стенографије за проглашавање Ваших формула. Следећа табела их сумира:
| Тип | редне (унутар текста) формуле | Приказане једначине | Приказане и аутоматски нумерисане једначине |
|---|---|---|---|
| Окружење | math
|
displaymath
|
equation
|
| LaTeX стенографија | \(...\)
|
\[...\]
|
|
| TeX стенографија | $...$
|
$$...$$
|
|
| Коментар | equation* (верзија са звездом) потискује нумеризацију, али захтева “amsmath”
|
Предлог: Коришћење овог $$...$$ треба заобићи, јер може проузроковати проблеме, посебно са “AMS-LaTeX” макросу. Штавише, ако се проблем појави, порука грешке неће бити од помоћи.
equation* и displaymath окружења су финкционално еквивалентна.
Ако нормално куцате текст, каже се да сте у тексту моду, али уколико куцате унутар једног од оних математичких окружења, каже се да сте у “математичком моду”', који се разликује од текст мода:
- Већина размака и нових редова немају никаквог значаја, пошто су сви размаци или изведени логички из математичких израза, или морају бити спецификовани посебним командама као што је
\quad - Празни редови нису дозвољени. Само један пасус по формули.
- Свако слово се сматра именом променљиве и биће писано као такво. Ако желите да пишете нормалан текст унутар формуле (нормалан раван фонт и нормални размаци), онда морате унети текст коришћењем посвећених команди.
Убацивање “приказане” математике унутар блокова текста
[уреди]Да би неки оператери, какви су \lim или \sum, били приказани исправно унутар неких математичких окружења (прочитајте $......$), може бити погодно писање \displaystyle класе унутар окружења. То може узроковати да линија буде дужа, али ће правилно приказати експоненте и индексе за неке математичке операторе. На пример, $\sum$ ће штампати мање Σ и $\displaystyle \sum$ ће штампати веће , као у једначинама (Ово ради само преко AMSMATH пакета). Такође, могуће је присилити овакво понашање за сва математичка окружења позивајући \everymath{\displaystyle} на самом почетку (тј. пре \begin{document}), што је корисно у дугачким документима.
Симболи
[уреди]У математици постоји доста симбола! Током учења LaTeXа, најтеже је запамтити како се који симбол штампа. Постоји, наравно, комплет симбола којима се може приступити директно са тастатуре:
+ - = ! / ( ) [ ] < > | ' :
Изван ових горе набројаних, посебне команде морају бити издате како би се приказали жељени симболи. Постоји много примера, као што су грчка слова, симболи релација, стрелице, бинарне операције итд.
На пример:
\forall x \in X, \quad \exists y \leq \epsilon
|
|
Срећом, постоји алат који може доста олакшати претрагу команди, за специфичне симболе. Тражите "Detexify" у одељку спољни линкови испод.
Грчка слова
[уреди]Грчка слова се често користе у математици, и веома се лако куцају у “математичком моду”. Само треба укуцати име слова после косе црте: ако је прво слово мало, добићете мало грчко слово, ако је прво слово велико (и само прво слово), добићете велико слово. Приметите да нека велика грчка слова изгледају као латинична, отдуа, није из обезбедио LaTeX (нпр. велика Alpha и Beta су само "A" и "B"). Мала слова епсилон, тета, капа, фи, пи, ро, и сигма су обезебеђена преко две различите верзије. Алтернативна, или '”'variant”, верзија се прави додавањем "var" пре имена слова:
\alpha, \Alpha, \beta, \Beta, \gamma, \Gamma, \pi, \Pi, \phi, \varphi, \Phi
|
|
Оператори
[уреди]Оператор је функција која је записана као реч: нпр. тригонометријске функције (sin, cos, tan), логаритми и експоненцијалне (log, exp), лимеси (lim), као и детерминанте (det). LaTeX има доста таквих, дефинисаних као команде:
\cos (2\theta) = \cos^2 \theta - \sin^2 \theta
|
|
За одеђене операторе као што су граничне вредности, ознака се налази испод оператора:
\lim_{x \to \infty} \exp(-x) = 0
|
|
За модуларне операторе постоје две команде: \bmod и \pmod:
a \bmod b
|
|
x \equiv a \pmod b
|
|
Степен и индекс
[уреди]Степени и индекси су еквивалентни суперскриптовима и сабскриптовима у нормалном текст моду. Знак за уметање (^) карактера се користи за подизање нечега, и доња црта (_) је за спуштање. Ако је више од једног израза подигнут или спуштен, они би требало да буду груписани користећи витичасте заграде ({ and }).
k_{n+1} = n^2 + k_n^2 - k_{n-1}
|
|
За степене, који имају више од једне цифре, окружите степен {}.
n^{22}
|
|
Доња црта (_) може бити коришћен са вертикалном траком () да означи евалуацију користећи сабскрипт запис у математици:
f(n) = n^5 + 4n^2 + 2 |_{n=17}
|
|
Разломци и биноми
[уреди]Разломак се прави \frac{numerator}{denominator} командом. (да потсетим, то су редом врх(бројилац) и дно(именилац)!). Исто тако, биномни коефицијент може бити записан коришћењем: \binom command[3]:
\frac{n!}{k!(n-k)!} = \binom{n}{k}
|
|
Такође, могуће је користити \choose команду без amsmath пакета:
\frac{n!}{k!(n-k)!} = {n \choose k}
|
|
Можете уградити разломке, унутар разломака:
\frac{\frac{1}{x}+\frac{1}{y}}{y-z}
|
|
Приметити да, када се појављује унутар другог разломка или у реду неког текста , разломак је знатно мањи него када се пише у математици. \tfrac и \dfrac команде[3] форсирају коришћење одговарајућих стилова, \textstyle или \displaystyle. Слично, \tbinom и \dbinom команде пишу биномне коефицијенте.
Други начин за писање разломака јесте коришћењем \over команде без amsmath пакета:
{n! \over k!(n-k)!} = {n \choose k}
|
|
За релативно једноставне разломке, посебно унутар текста, можда буде естетски боље користити степене и индексе:
^3/_7
|
|
Ако изгледа мало “опуштено” (превелики размак), ужа верзија може бити дефинисана убацивањем негативног размака
%покретање разломака косом цртом – захтева математички мод.
\newcommand*\rfrac[2]{{}^{#1}\!/_{#2}}
\rfrac{3}{7}
|
|
Ако планирате да га користите кроз цео документ, препоручује се xfrac пакет.
Пакет обезбеђује \sfrac команду, да створи косе разломке. Употреба:
Узмите $\sfrac{1}{2}$ шоље шећера, \dots
3\times\sfrac{1}{2}=1\sfrac{1}{2}
Узмите ${}^1/_2$ шоље шећера, \dots
3\times{}^1/_2=1{}^1/_2
|
Ако се разломци користе као експоненте, витичасте заграде морају бити коришћене око \sfrac команде:
$x^\frac{1}{2}$ % нема грешке
$x^\sfrac{1}{2}$ % грешка
$x^{\sfrac{1}{2}}$ % нема грешке
$x^\frac{1}{2}$ % no error
|
|
У неким случајевима, коришћење само пакета резултираће грешкама о одређеним недоступним облицима фонтова. У том случају, lmodern и fix-cm пакети морају бити такође убачени.
Алтернативно, nicefrac пакет обезбеђује \nicefrac команду, која се користи слично као и \sfrac.
Континуирани разломци
[уреди]Континуиране разломке треба писати коришћењем \cfrac команде[3]:
\begin{equation}
x = a_0 + \cfrac{1}{a_1
+ \cfrac{1}{a_2
+ \cfrac{1}{a_3 + \cfrac{1}{a_4} } } }
\end{equation}
|
|
Множење два броја
[уреди]Да би множење направили визуелно сличним разломку, угњеждени низ може бити коришћен, на пример, множење бројева написаних један испод другог.
\begin{equation}
\frac{
\begin{array}[b]{r}
\left( x_1 x_2 \right)\\
\times \left( x'_1 x'_2 \right)
\end{array}
}{
\left( y_1y_2y_3y_4 \right)
}
\end{equation}
|
|
Корен
[уреди]\sqrt команда прави квадратни корен, који окружује израз. Прихвата опциони аргумент, који је спецификован у угластим заградама ([ и ]), како би променио величину:
\sqrt{\frac{a}{b}}
|
|
\sqrt[n]{1+x+x^2+x^3+\ldots}
|
|
Неки људи воле писање квадратног корена затварањем истог преко његовог садржаја. Овај метод чини јаснијим оно што се налази у простору коренског знака. Ова навика се не користи често када пишемо преко компјутера, али ако још увек хоћете да промените излаз квадратног корена, LaTeX Вам даје ту могућност. Само додајте следећи код у уводу вашег документа:
Овај TeX код прво преименује \sqrt команду као \oldsqrt, онда поново дефинише \sqrt у условима старог, додавањем нечега више. Нови квадратни корен се може видети на слици на левој, у поређењу са старим на десној страни. Нажалост, овај код неће радити ако желите вишеструке коренове: ако покушате да напишете као \sqrt[b]{a}} \LetLtxMacro{\oldsqrt}{\sqrt} \renewcommand*{\sqrt}[2][\ ]{\oldsqrt[#1]{#2} } \makeatother $\sqrt[a]{b} \quad \oldsqrt[a]{b}$
Међутим, ово захтева \usepackage{letltxmacro} пакет
Суме и интеграли
[уреди]\sum и \int команде редом убацују суму и интеграл, са границама обележеним каретом (^) и доњом цртом (_). Типичне нотације за суму су:
\sum_{i=1}^{10} t_i
|
|
или
\displaystyle\sum_{i=1}^{10} t_i
|
|
Границе интеграла се пишу по истом принципу. Такође је битно претставити интеграционе промењиве усправним “d”, што се, у математичком моду, одржава кроз \mathrm{} команду, и одвојити је малим разломком од остатка интеграла, што се постиже \, командом.
\int_0^\infty \mathrm{e}^{-x}\,\mathrm{d}x
|
|
Постоје и друге "велике" команде које функционишу на сличан начин:
\sum |
\prod |
\coprod |
|||||
\bigoplus |
\bigotimes |
\bigodot |
|||||
\bigcup |
\bigcap |
\biguplus |
|||||
\bigsqcup |
\bigvee |
\bigwedge |
|||||
\int |
\oint |
\iint[3] |
|||||
\iiint[3] |
\iiiint[3] |
\idotsint[3] |
За више интеграционих симбола, укључујући и оне који нису саджане уобичајним компјутер модерним фонтом, пробајте esint пакет.
\substack команда[3] дозвољава коришћење \\, за писање граница у више редова:
\sum_{\substack{
0<i<m \\
0<j<n
}}
P(i,j)
|
|
Ако желите да границе интеграла буду конкретно изнад и испод симбола (као код суме), користите \limits команду:
\int\limits_a^b
|
|
Међутим, ако желите да ово ради за СВЕ интегралеHowever, пожељно је да спецификујете intlimits опцију, при учитавању amsmath пакета:
\usepackage[intlimits]{amsmath}
|
За веће интеграле, можете корстити личне декларације, или bigints пакет [4].
Заграде
[уреди]Како користити заграде у једначинама, које се простиру у више редова, описано је LaTeX/Напреднија математика поглављу.
Употреба граничника, као што су загдаре, постаје битна када се суочавате са било чим, па чак и тривијалним једначинама. Без њих, формуле могу постати двосмислене. Такође, посебни типови математичких структура, какве су матрице, типично се ослањају на граничнике, који би их затворили.
Постоји велики избор доступних граничника у LaTeXу:
( a ), [ b ], \{ c \}, | d |, \| e \|,
\langle f \rangle, \lfloor g \rfloor,
\lceil h \rceil, \ulcorner i \urcorner
|
|
где се \lbrack и \rbrack могу користити уместо [ and ].
Аутоматско димензионисање
[уреди]Веома често ће се, математичке особине, разликовати у величини, у том случају, граничници, који окружују израз, треба адекватно да варирају. Ово се може аутоматски постићи коришћењем \left, \right, и \middle команди. Било који, од претходних граничника, се могу користити у комбинацији са овим:
\left(\frac{x^2}{y^3}\right)
|
|
P\left(A=2\middle|\frac{A^2}{B}>4\right)
|
Витичасте заграде се различито дефинишу коришћењем \left\{ и \right\},
\left\{\frac{x^2}{y^3}\right\}
|
|
Ако је граничник потребан само на једној страни израза, онда се невидљиви граничник на другој страни може написати коришћењем периода (.).
\left.\frac{x^3}{3}\right|_0^1
|
|
Ручно димензионисање
[уреди]У одређеним ситуацијама, димензионисање одрађено од \left и \right команди, може да не буде пожељно, или можете, једноставно, желети финију контролу граничних величина. У том случају, \big, \Big, \bigg и \Bigg модификаторске команде могу бити коришћене:
( \big( \Big( \bigg( \Bigg(
|
|
Ове команде се примарно корисне када се суочавате са угнежђеним граничницима. На пример, за време писања
\frac{\mathrm d}{\mathrm d x} \left( k g(x) \right)
|
|
приметимо да \left и \right команде дају исте граничнике као и они угнежђени. Да бисмо ово поправили, пишемо
\frac{\mathrm d}{\mathrm d x} \big( k g(x) \big)
|
|
Ручно димензионисање може, такође, бити корисно када је једначина превелика, протеже се до краја странице, и мора се поделити у два реда коришћењем усклађене команде. Иако, команде \left. и \right. могу бити коришћене за баланцирање граничника у сваком реду, ово може довести до погрешних гричних величина. Штавише, ручно димензионисање може бити коришћено за избегавање превише великих граничника ако се \underbrace или слична команда појави између граничника.
Куцање интервала
[уреди]За означавање отворених и полу отворених интервала, користе се ознаке ]a,b[, (a,b), ]a,b], (a,b], [a,b[ и [a,b). Ако се користи угласта заграда, онда се интервал мора ставити између витичастих заграда ({ and }), како би имали тачан размак. Слично, ако (полу)отворен интервал почиње негативним бројем, онда тај број, укључујући и знак “минус” мора бити стављен у витичасте заграде, тако да LaTeX разуме да је “минус” симбол унарна операција. Упоредите:
x \in [-1,1]
|
|
x \in {[-1,1]}
|
|
x \in {[{-1},1]}
|
|
Матрице и низови
[уреди]Основна матрица може бити креирана користећи matrix окружење[3]: заједно са другим табличним структурамаin, улази се спецификују редом, са колонама одвојеним коришћењем амперсенда (&) и новим редовима, одвојеним дуплом косом цртом (\\)
\begin{matrix}
a & b & c \\
d & e & f \\
g & h & i
\end{matrix}
|
|
Да бисте наместили поравнање колона у табели, користите верзију са звездицом[5]:
\begin{matrix}
-1 & 3 \\
2 & -4
\end{matrix}
=
\begin{matrix*}[r]
-1 & 3 \\
2 & -4
\end{matrix*}
|
|
Поравнање по “дифолту” је c, али може бити било који валидан тип колоне у array окружењу.
Међутим, матрице су обично затворене у граничницима неке врсте, и док је могуће користити \left и \right commands, постоје многобројна друга дефинисана окружења, која аутоматски укључују граничнике:
| Име окљужења | Заграде које окружују | Бележке |
|---|---|---|
| pmatrix[3] | центрира колоне по “дифолту” | |
| pmatrix*[5] | омогућава да одредите поравнање колона у опционим параметрима | |
| bmatrix[3] | центрира колоне по “дифолту” | |
| bmatrix*[5] | омогућава да одредите поравнање колона у опционим параметрима | |
| Bmatrix[3] | центрира колоне по “дифолту” | |
| Bmatrix*[5] | омогућава да одредите поравнање колона у опционим параметрима | |
| vmatrix[3] | центрира колоне по “дифолту” | |
| vmatrix*[5] | омогућава да одредите поравнање колона у опционим параметрима | |
| Vmatrix[3] | центрира колоне по “дифолту” | |
| Vmatrix*[5] | омогућава да одредите поравнање колона у опционим параметрима |
За време писања матрица произвољних величина, уобичајно је користити хоризонталне, вертикалне и дијагоналне триплете тачака, како би испунили одређене колоне и редове. Ово се може спецификовати коришћењем редом \cdots, \vdots и \ddots:
A_{m,n} =
\begin{pmatrix}
a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\
a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m,1} & a_{m,2} & \cdots & a_{m,n}
\end{pmatrix}
|
|
У неким ситуацијама, можда ћете желети финију контролу равнања унутар сваке колоне, или можда желети да убаците редове између колона или редова. Ово се може постићи коришћењен array окружења, што је, суштински, математичка верзија tabular environment, које захтева да колоне буду претходно наведене:
\begin{array}{c|c}
1 & 2 \\
\hline
3 & 4
\end{array}
|
|
Можете видети да AMS матрична класа окружења не оставља довољно простора, када се користи истовремено са разломцима, резултирајући излаз сличан овоме:
Да бисте контрирали овом проблему, убаците додатни простор са опционим параметром у \\ команду:
M = \begin{bmatrix}
\frac{5}{6} & \frac{1}{6} & 0 \\[0.3em]
\frac{5}{6} & 0 & \frac{1}{6} \\[0.3em]
0 & \frac{5}{6} & \frac{1}{6}
\end{bmatrix}
|
|
Ако вам затребају "границе" или "индекси" у матрици, основни TeX обезбеђује макро \bordermatrix
M = \bordermatrix{~ & x & y \cr
A & 1 & 0 \cr
B & 0 & 1 \cr}
|
Матрице у тексту
[уреди]Како бисте убацили мало матрицу, а да притом не повећате ред који је садржи, користите smallmatrix окружење:
Матрица у тексту мора бити мања:
$\bigl(\begin{smallmatrix}
a&b \\ c&d
\end{smallmatrix} \bigr)$
како не би повећала текст.
|
Rendering missing! |
Додавање текста у једначинама
[уреди]Математичко окружење се разликује од текстуалног у представљању текста. Ево примера за покушај приказивања текста унутар математичког окружења:
50 јабука \times 100 јабука = доста јабука^2
|
|
Постоје два приметна проблема: нема размака између речи или бројева, и слова су у “италик” фонту и са већим размаком него обично. Оба проблема су, једноставно, артефакти математичког мода, у којем се опходи према њима као математичким исказима: размаци су игнорисани (LaTeX ставља размаке у математици по својим правилима), и сваки карактер је одвојен елемент (тако да нису позиционирани толико блиско као у нормалном тексту).
Постоји више начина за тачно додавање текста. Типичан начин јесте “замотавање” текста \text{...} командом [3] (слична команда је \mbox{...}, премда ово ствара проблеме са сабскриптом, и има мање описно име). Да видимо шта се догађа када је горња једначина адаптирана:
50 \text{јабука} \times 100 \text{јабука}
= \text{доста јабука}^2
|
|
Текст изгледа боље. Међутим, нема празнина између бројева и слова. Нажалост, дужни сте да их експлицитно додате. Постоји доста начина за додавање размака између математичких елемената, али због једноставности можемо само додати размак у \text команду.
50 \text{ јабука} \times 100 \text{ јабука}
= \text{доста јабука}^2
|
|
Форматиран текст
[уреди]Коришћење \text је у реду и даје основни резултат. Ипак, постоји алтернатива која даје већу флексибилност. Можете се вратити на увод команди за форматирање фонтова, као што су \textrm, \textit, \textbf, итд. Ове команде тачно форматирају аргументе, нпр., \textbf{bold text} даје болдирани текст. Ове команде су једнако валидне унутар математичког окружења, када је у питању убацивање текста. Предност овога јесте у томе што можете имати бољу контролу око форматирања фонтова (слова), више него у стандардном тексту унутар \text.
50 \textrm{ јабука} \times 100
\textbf{ јабука} = \textit{доста јабука}^2
|
|
Форматирање математичких симбола
[уреди]Сада можемо да форматирамо текст; али шта је са форматирањем математичких израза? Постоји комплет команди форматирања, који је веома сличан управо коришћеном форматирању фонта, осим што су специфично циљани на текст у математичком моду (захтевају amsfonts)
| LaTeX команда | Узорак | Опис | Честа употреба |
|---|---|---|---|
\mathnormal{…}(или једноставно изоставити било коју команду) |
Обичан математички фонт | Већина математичких нотација | |
\mathrm{…}
|
Ово је обичан или нормалан фонт, без “италика” | Мерне јединице, функције сачињене од једне речи(тригонометрија) | |
\mathit{…}
|
“Италик” фонт | Функције сачињене од више слова или имена варијабли. У поређењу са \mathnormal, речи су одвојене природније и бројеви су, такође, на “италик” фонту.
| |
\mathbf{…}
|
“Болд” фонт | Вектори | |
\mathsf{…}
|
Бесерифни | ||
\mathtt{…}
|
”Моноспејс” фонт | ||
\mathfrak{…}
|
Фрактур | Скоро канонски фонт за алгебру, са супскриптом која се користи да означи папире Новог Завета, идеала у теорији прстена. | |
\mathcal{…}
|
Калиграфија (само велика слова) | Често се користи за снопове/шеме и категорије, користи се да означи криптографичке концепте као што је алфабет дефиниција (), простор поруке (), простор шифрата () and простор кључева (); “Клиново” ]]; “давање имена конвенцијама у описној логици”; Лапласова трансформација () и Фуријеов ред () | |
\mathbb{…}(захтева amsfonts или amssymb пакет) |
”Блекборд” болд (само велика слова) | Користи се за означавање специјалних комплета (нпр. реалних бројева) | |
\mathscr{…}(захтева mathrsfs пакет) |
Скрипта (само велика слова) | Алтернативни фонт за категорије и шеме. |
Ево команде форматирања могу “окружити” читаве једначине, и то не само на текстуалним елементима: они само форматирају слова, бројеве и велика грчка слова, и остале математичке команде су непромењене.
Болдирана мала грчка слова или остали симболи користе \boldsymbol команду[3]; ово ће само радити ако постоји “болд” верзија симбола у тренутном фонту. Као последње уточиште постоји \pmb команда[3] (“болд” сиромашног човека): ово штампа више верзија карактера који се мало разликују један од другог.
\boldsymbol{\beta} = (\beta_1,\beta_2,\dotsc,\beta_n)
|
|
Акценти
[уреди]Шта радити када останете без симбола и фонтова? Следећи корак је коишћење акцената:
a' or a^{\prime} |
a'' |
||
\hat{a} |
\bar{a} |
||
\grave{a} |
\acute{a} |
||
\dot{a} |
\ddot{a} |
||
\not{a} |
\mathring{a} |
||
\overrightarrow{AB} |
\overleftarrow{AB} |
||
a''' |
a'''' |
||
\overline{aaa} |
\check{a} |
||
\breve{a} |
\vec{a} |
||
\dddot{a}[3] |
\ddddot{a}[3] |
||
\widehat{AAA} |
\widetilde{AAA} |
||
\widehat{AAA} |
\stackrel\frown{AAA} |
||
\tilde{a} |
\underline{a} |
Боја
[уреди]Пакет xcolor, описан у Боје, дозвољава нам додавање боје нашој једначини. На пример,
k = {\color{red}x} \mathbin{\color{blue}-} 2
|
|
Једини проблем је што ово ремети уобичајно LaTeX форматирање око - оператора. Да би поправили ово, ми га ограђујемо у \mathbin окружењу, пошто је - бинарна операција. Овај процес је описан овде.
Плус и минус знаци
[уреди]LaTeX се носи са + и − знацима на два могућа начина. Најучесталији је бинарни оператор. Када се два математичка елемента појаве на било којој страни знака, претпоставља се да је у питању бинарна операција, и као таква, додељује размак на обе стране знака. Алтернативни начин је именовање знака. Ово је када означавате да ли је математичка једнакост позитивна или негативна. Ово је уобичајно за оно друго, пошто у математици, сви елементи се рачунају као позитивни, осим ако немају − префикс испред. У овом случају, желите да се знак појави близу одговарајућег елемента, како би показао њихову повезаност. Ако ставите + или − без ичега пре њега, али желите да се њим барата као бинарном операцијом, можете додати “невидљив” карактер пре оператора користећи {}. Ово може бити корисно ако пишете формуле у неколико редова, а нови ред почиње са = или +, на пример, онда можете поправити необична поравнања додавајући невидљиви карактер тамо где је то потребно.
Плус-минус знак се пише као:
\pm
|
|
Слично томе, такође, постоји минус-плус знак:
\mp
|
|
Контрола хоризонталног размака
[уреди]LaTeX је, очигледно, веома добар у писању математике—то је био један од главних циљева језгра TeX система који LaTeX продужује. Међутим, не може се увек на њега ослонити да јасно интерпретира формуле, на начин на који сте Ви то урадили. Мора да направи одређене претпоставке када има двосмислених израза. Резултат може бити некоректан у смислу хоризонталног размака. У тим случајевима, излаз је још увек задовољавајући, ипак перфекционисти ће, без сумње, желети да фино подесе своје формуле, како би осигурали правилне хоризонталне размаке. Ово су, генерално, веома суптилна прилагођавања.
Постоје други случајеви, где је LaTeX коректно обавио свој посао, али само желите да додате мало размака, можда додате коментар неки. На пример, у следећој једначини, пожељно је осигурати да постоји одређен размак између математике и текста.
\[ f(n) =
\begin{cases}
n/2 & \quad \text{if } n \text{ is even}\\
-(n+1)/2 & \quad \text{if } n \text{ is odd}\\
\end{cases}
\]
|
|
Овај код избацује грешку ако користите Miktex 2.9 и не избацује резултат, који је виђен као тачан. Користите \mathrm уместо само \text.
(Приметити да конкретно овај пример може бити изражен елегантнијим кодом коришћењем cases окружења, обезбеђеног од amsmath пакета описаног у поглављу Напреднија математика.)
LaTeX је дефинисао две команде које могу бити коришћене за убацивање хоризонталног размака било где у документу (не само у математици). То су \quad и \qquad
\quad је размак једнак величини фонта. Дакле, ако користите “11pt” фонт, онда ће размак, обезбеђен од \quad, такође бити “11pt” (наравно, хоризонтално). \qquad даје дупло већи размак од фонта. Као што можете видети из кода, у претходном примеру, \quad-ови су коришћени за додавање размака између математике и текста.
Дакле, враћамо се на фино подешавање поменуто на почетку документа. Добар пример би био показивање једноставне једначине недефинисаног интеграла.
Ако ћете ово покушати, можете и написати:
\int y \mathrm{d}x
|
|
Међутим, ово не даје коректан резултат. LaTeX не поштује размак остављен у коду који означава да су y и dx независни ентитети. Уместо тога, он их спаја све заједно. \quad би, очигледно, био “претучен” у овој ситуацији—оно што је потребно јесу мали размаци који ће бити коришћени у оваквом примеру, и то је оно што LaTeX пружа:
| Команда | Опис | Величина |
|---|---|---|
\,
|
мали размак | 3/18 “quad”-а |
\:
|
средњи размак | 4/18 “quad”-а |
\;
|
велики размак | 5/18 “quad”-а |
\!
|
негативни размак | -3/18 “quad”-а |
Напомена: можете користити више од једне команде уколико Вам је потребан већи размак.
Дакле, да исправимо тренутни проблем:
\int y\, \mathrm{d}x
|
|
\int y\: \mathrm{d}x
|
|
\int y\; \mathrm{d}x
|
|
Негативни размак можда делује као чудна ствар за коришћење, међутим, не би било ту да од њега нема “неке” користи! Узмите следећи пример:
\left(
\begin{array}{c}
n \\
r
\end{array}
\right) = \frac{n!}{r!(n-r)!}
|
|
Матрични исказ за приказивање биномних коефицијената је превише тапациран. Превилики је размак између заграде и саржаја унутар истих. Ово се лако може исправити додавањем пар негативних размака, после леве и пре десне заграде.
\left(\!
\begin{array}{c}
n \\
r
\end{array}
\!\right) = \frac{n!}{r!(n-r)!}
|
|
У сваком случају, ручно додавање размака треба избегавати кад год је то могуће: то чини изворни код комплекснијим и у супротности је са основним принципом “То што видиш је оно на шта си мислио” приступа. Најбоља ствар за чинити јесте дефинисање неких команди користећи све размаке које желите и онда, када користите своју команду, не треба да додајете више размаке. Касније, ако се предомислите када је у питању дужина хоризоналног размака, лако га можете променити, модификовањем команде коју сте раније дефинисали. Хајде да ово покажемо на примеру: ако желите d од dx у интегралу да буде у римском фонту и мало раздвојено од остатка. Ако желите да напишете овакав интеграл \int x \, \mathrm{d} x, можете дефинисати овакву команду:
\newcommand{\dd}{\mathop{}\,\mathrm{d}}
|
у уводу вашег документа. Изаврали смо \dd само зато што потсећа да је "d" замењено и зато што је брзо за куцање. На тај начин, код Вашег интеграла постаје \int x \dd x. Сада, када год пишете интеграл, само морате да користите \dd уместо "d", и сви Ваши интеграли ће имати исти стил. Ако се предомислите, само треба да промените дефиницију у уводу, и сви Ваши интеграли ће се променити по дефиницији.
Ручно одређивање стила формуле
[уреди]Да ручно прикажете фрагмент формуле користећи тесктуални стил, окружите фрагмент витичастим заградама и ставите префикс фрагменту уз помоћ \textstyle. Заграде су обавезне због \textstyle макро мења стање приказивача, приказивајући све остале делове математике у текстуалном стилу. Заграде лимитирају промену стања на само фрагмент у истим. На пример, за коришћење текстуалног стила само за збир симбола у суми, унели бисте
\begin{equation}
C^i_j = {\textstyle \sum_k} A^i_k B^k_j
\end{equation}
|
Иста ствар, али као команда, изгледала би овако:
\newcommand{\tsum}[1]{{\textstyle \sum_{#1}}}
|
Приметите додатне заграде. Само један пар око израза неће бити довољан. То би изазвало да свака каснија математика \tsum k буде приказана коришћењем текстуалног стила.
Да прикажете део формуле, коришћењем приказивачког стила, урадите исту ствар, али користите \displaystyle.
Напреднија математика: “AMS Math” пакет
[уреди]“AMS” (“American Mathematical Society”) математички пакет јесте моћан пакет који прави виши слој апстракција у математичком LaTeX језику; ако га користите, олакшаће Вам живот. Неке уведене команде amsmath пакета ће учини да друге основне LaTeX команде делују застарело: како бисте одржавали константност у финалном излазу, боље би било да користите amsmath команде, кад год је то могуће. Ако тако учините, добићете елегантан излаз без бриге о поравнању и другим детаљима, чинећи изворни код читким. Ако желите да га корисистите, у увод морате ово да убаците:
\usepackage{amsmath}
|
Увођење тачака у формуле
[уреди]amsmath дефинише такође \dots команду, што је генерализација већ постојеће \ldots. Можете користити \dots и у текстуалном и математичком моду и LaTeX ће је заменити са три тачке "…" , али ће одлучити на основу контекста да ли да га стави на дну као (као \ldots) или центирано (као \cdots).
Тачке
[уреди]LaTeX даје неколико команди за убацивање тачака (елипси) у Вашу формулу. Ово може бити посебно корисно ако пишете велике матрице и избегавате елементе. Пре свега, ево основни команди везаних за тачке које LaTeX обезбеђује:
| Код | Излаз | Коментар |
|---|---|---|
\dots |
опште тачке , коришћене у тексту (такође, изван формуле). Аутоматски сређује размаке пре и после себе, по контексту, то је команда вишег реда. | |
\ldots |
излаз је сличан претходном, али нема аутоматског сређивања размака; ради на нижем нивоу. | |
\cdots |
Тачке су центриране релативно у односу на висину слова. Такође, постоји бинарни оператор множења, \cdot, поменут испод.
| |
\vdots |
Вертикалне тачке. | |
\ddots |
Дијагоналне тачке. | |
\iddots |
Инверзне дијагоналне тачке (захтевају mathdots пакет). | |
\hdotsfor{n} |
Користе се у матрицама, прави ред тачака које се шире кроз n колона. |
Уместо коришћења \ldots и \cdots, треба да користите семантички оријентисане команде. Тиме постаје могуће, у лету, адаптирати свој документ другачијим конвенцијама, у слчају (на пример) да ,прате да пошаљете издавачу који инсистира на праћењу “кућне” традиције. Уобичајни третман за различите врсте прати конвенције Америчког друштва математичара.
Листа математичких симбола
[уреди]Сви дефинисани математички симболи из \TeX\ пакета набројани су испод. Још симбола је доступно из додатних пакета.
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
<
|
>
|
=
|
\parallel
|
\nparallel
| |||||||||
\leq
|
\geq
|
\doteq
|
\asymp
|
\bowtie
| |||||||||
\ll
|
\gg
|
\equiv
|
\vdash
|
\dashv
| |||||||||
\subset
|
\supset
|
\approx
|
\in
|
\ni
| |||||||||
\subseteq
|
\supseteq
|
\cong
|
\smile
|
\frown
| |||||||||
\nsubseteq
|
\nsupseteq
|
\simeq
|
\models
|
\notin
| |||||||||
\sqsubset
|
\sqsupset
|
\sim
|
\perp
|
\mid
| |||||||||
\sqsubseteq
|
\sqsupseteq
|
\propto
|
\prec
|
\succ
| |||||||||
\preceq
|
\succeq
|
\neq
|
\sphericalangle
|
\measuredangle
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | |||
|---|---|---|---|---|---|---|---|---|---|---|
\pm
|
\cap
|
\diamond
|
\oplus
| |||||||
\mp
|
\cup
|
\bigtriangleup
|
\ominus
| |||||||
\times
|
\uplus
|
\bigtriangledown
|
\otimes
| |||||||
\div
|
\sqcap
|
\triangleleft
|
\oslash
| |||||||
\ast
|
\sqcup
|
\triangleright
|
\odot
| |||||||
\star
|
\vee
|
\bigcirc
|
\circ
| |||||||
\dagger
|
\wedge
|
\bullet
|
\setminus
| |||||||
\ddagger
|
\cdot
|
\wr
|
\amalg
|
| Symbol | Script | Symbol | Script | |
|---|---|---|---|---|
\exists
|
\rightarrow or \to
| |||
\nexists
|
\leftarrow or \gets
| |||
\forall
|
\mapsto
| |||
\neg
|
\implies
| |||
\subset
|
\Rightarrow or \implies
| |||
\supset
|
\leftrightarrow
| |||
\in
|
\iff
| |||
\notin
|
\Leftrightarrow (preferred for equivalence (iff))
| |||
\ni
|
\top
| |||
\land
|
\bot
| |||
\lor
|
and | \emptyset and \varnothing
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | |||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
\|
|
/
|
\backslash
| |||||||
\{
|
\}
|
\langle
|
\rangle
| |||||||
\uparrow
|
\Uparrow
|
\lceil
|
\rceil
| |||||||
\downarrow
|
\Downarrow
|
\lfloor
|
\rfloor
|
Белешка: За коришћење грчких слова у LaTeXу, која имају исти изглед као њихови римски еквиваленти, само користите римску форму: e.g., “A” уместо “Alpha”, “B” уместо “Beta”, итд.
| Symbol | Script | Symbol | Script | |
|---|---|---|---|---|
| and | A and \alpha
|
and | N and \nu
| |
| and | B and \beta
|
and | \Xi and \xi
| |
| and | \Gamma and \gamma
|
and | O and o
| |
| and | \Delta and \delta
|
, and | \Pi, \pi and \varpi
| |
| , and | E, \epsilon and \varepsilon
|
, and | P, \rho and \varrho
| |
| and | Z and \zeta
|
, and | \Sigma, \sigma and \varsigma
| |
| and | H and \eta
|
and | T and \tau
| |
| , and | \Theta, \theta and \vartheta
|
and | \Upsilon and \upsilon
| |
| and | I and \iota
|
, , and | \Phi, \phi and \varphi
| |
| , and | K, \kappa and \varkappa
|
and | X and \chi
| |
| and | \Lambda and \lambda
|
and | \Psi and \psi
| |
| and | M and \mu
|
and | \Omega and \omega
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
\partial
|
\imath
|
\Re
|
\nabla
|
\aleph
| |||||||||
\eth
|
\jmath
|
\Im
|
\Box
|
\beth
| |||||||||
\hbar
|
\ell
|
\wp
|
\infty
|
\gimel
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | |||
|---|---|---|---|---|---|---|---|---|---|---|
\sin
|
\arcsin
|
\sinh
|
\sec
| |||||||
\cos
|
\arccos
|
\cosh
|
\csc
| |||||||
\tan
|
\arctan
|
\tanh
|
||||||||
\cot
|
\arccot
|
\coth
|
Резиме
[уреди]Као што можете видети, куцање математике може бити понекад тешко. Међутим, јер LaTeX нуди толико контроле, можете добити веома професионално откуцану математику са релативно мало труда (када уђете у штос, наравно!). Било би могуће наставити са темом математике, јер делује као да нема крај. Међутим, овим “туторијалом”, требало би брзо да ухватите прикључак.
Белешке
[уреди]- ↑ http://www.ams.org/publications/authors/tex/amslatex
- ↑ http://www.ctan.org/tex-archive/macros/latex/contrib/mathtools/mathtools.pdf
- ↑ 3,00 3,01 3,02 3,03 3,04 3,05 3,06 3,07 3,08 3,09 3,10 3,11 3,12 3,13 3,14 3,15 3,16 3,17 3,18 requires the amsmath package
- ↑ http://hdl.handle.net/2268/6219
- ↑ 5,0 5,1 5,2 5,3 5,4 5,5 requires the mathtools package
Спољни линкови
[уреди]- LaTeX maths symbols
- detexify: applet for looking up LaTeX symbols by drawing them
- amsmath documentation
- LaTeX - The Student Room
- The Comprehensive LaTeX Symbol List
- MathLex - LaTeX math translator and equation builder

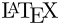























![{\displaystyle {\sqrt[{n}]{1+x+x^{2}+x^{3}+\ldots }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c20a0cedb6864fce2fb1395a58699288b7a507b0)

![{\displaystyle {\sqrt[{b}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ceeccbbf1609652afdb8d84d33552cd2731bb0d)























![{\displaystyle (a),[b],\{c\},|d|,\|e\|,\langle f\rangle ,\lfloor g\rfloor ,\lceil h\rceil ,\ulcorner i\urcorner }](https://wikimedia.org/api/rest_v1/media/math/render/svg/61234d9b478821fe1f357388b1f4f098e5745b81)






![{\displaystyle x\in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722)
![{\displaystyle x\in {[-1,1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a18934c1ca2e4c5a3b42159017fb6fef2e3d9b4b)
![{\displaystyle x\in {[{-1},1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15fe4946dcbe93e3bf8fca8fa5d70bb39da0eee2)



![{\displaystyle [\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5444b5227fcebf7e7cbb9ee114af1373f6a2e95)






![{\displaystyle M={\begin{bmatrix}{\frac {5}{6}}&{\frac {1}{6}}&0\\[0.3em]{\frac {5}{6}}&0&{\frac {1}{6}}\\[0.3em]0&{\frac {5}{6}}&{\frac {1}{6}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4989d4433782a036095cdf274ee636c5f783125c)































































































































































































































































