LaTeX/Matematika
Jedna od najvećih motivacionih sila Donalda Knuta, kada je počeo da razvija originalni TeX sistem, jeste bila bila pravljenje nečega što je omogućavalo lako konstrukciju matematičkih formula, ali da izgleda profesinalno kad se odštampa. Činjenica da je uspeo u svojoj nameri je najverovatnije razlog zbog kojeg je TeX (i kasnije, LaTeX) postao toliko popularan u naučnom društvu. Kucanje matematike je jedna od najvećih LaTeXovih vrlina. To je, takođe, velika tema zbog postojanja toliko matematičkih notacija.
Ako Vaš dokument zahteva samo nekoliko jednostavnih matematičkih formula, običan LaTeX ima većinu potrebnih alata. Ako pišete naučni dokument koji sadrži veliko broj komplikovanih formula, amsmath package[1] uvodi nekoliko novih komandi koje su jače i fleksibilnije od onih koje daje LaTeX. mathtools popravlja neke amsmath nedostatke i dodaje korisna podešavanja, simbole, i okruženja amsmath-u.[2] Za korišćenje ili jednog ili drugog paketa, otkucajte:
\usepackage{amsmath}
ili
\usepackage{mathtools}
u uvodu Vašeg teksta. mathtools paket učitava amsmath paket i otuda nema potrebe za \usepackage{amsmath} u uvodu, ako je mathtools korišćen.
Matematička okruženja
[uredi]LaTeX mora da zna da naknadni tekst zaista sadrži matematičke elemente. To je zato što LaTeX kuca metamatičke notacije drugačije od običnog teksta. Stoga, posebna okruženja su napravljena iz ovog razloga. Mogu se podeliti na dve kategorije u zavisnosti od toga kako će biti prezentovane:
- text — tekstualne formule se redno prikazuju, to jest, unutar tela teksta u kojem je proglašena, na primer, mogu reći da je a + a = 2a unutar ove rečenice.
- displayed — prikazuje formule koje su odvojene od glavnog teksta.
Kako matematika zahteva posebna okruženja, postoje, naravno, odgovarajuća imena okruženja koja možete standardno koristiti. Za razliku od ostalih okruženja, međutim, postoje neke zgodne stenografije za proglašavanje Vaših formula. Sledeća tabela ih sumira:
| Tip | redne (unutar teksta) formule | Prikazane jednačine | Prikazane i automatski numerisane jednačine |
|---|---|---|---|
| Okruženje | math
|
displaymath
|
equation
|
| LaTeX stenografija | \(...\)
|
\[...\]
|
|
| TeX stenografija | $...$
|
$$...$$
|
|
| Komentar | equation* (verzija sa zvezdom) potiskuje numerizaciju, ali zahteva “amsmath”
|
Predlog: Korišćenje ovog $$...$$ treba zaobići, jer može prouzrokovati probleme, posebno sa “AMS-LaTeX” makrosu. Štaviše, ako se problem pojavi, poruka greške neće biti od pomoći.
equation* i displaymath okruženja su finkcionalno ekvivalentna.
Ako normalno kucate tekst, kaže se da ste u tekstu modu, ali ukoliko kucate unutar jednog od onih matematičkih okruženja, kaže se da ste u “matematičkom modu”', koji se razlikuje od tekst moda:
- Većina razmaka i novih redova nemaju nikakvog značaja, pošto su svi razmaci ili izvedeni logički iz matematičkih izraza, ili moraju biti specifikovani posebnim komandama kao što je
\quad - Prazni redovi nisu dozvoljeni. Samo jedan pasus po formuli.
- Svako slovo se smatra imenom promenljive i biće pisano kao takvo. Ako želite da pišete normalan tekst unutar formule (normalan ravan font i normalni razmaci), onda morate uneti tekst korišćenjem posvećenih komandi.
Ubacivanje “prikazane” matematike unutar blokova teksta
[uredi]Da bi neki operateri, kakvi su \lim ili \sum, bili prikazani ispravno unutar nekih matematičkih okruženja (pročitajte $......$), može biti pogodno pisanje \displaystyle klase unutar okruženja. To može uzrokovati da linija bude duža, ali će pravilno prikazati eksponente i indekse za neke matematičke operatore. Na primer, $\sum$ će štampati manje Σ i $\displaystyle \sum$ će štampati veće , kao u jednačinama (Ovo radi samo preko AMSMATH paketa). Takođe, moguće je prisiliti ovakvo ponašanje za sva matematička okruženja pozivajući \everymath{\displaystyle} na samom početku (tj. pre \begin{document}), što je korisno u dugačkim dokumentima.
Simboli
[uredi]U matematici postoji dosta simbola! Tokom učenja LaTeXa, najteže je zapamtiti kako se koji simbol štampa. Postoji, naravno, komplet simbola kojima se može pristupiti direktno sa tastature:
+ - = ! / ( ) [ ] < > | ' :
Izvan ovih gore nabrojanih, posebne komande moraju biti izdate kako bi se prikazali željeni simboli. Postoji mnogo primera, kao što su grčka slova, simboli relacija, strelice, binarne operacije itd.
Na primer:
\forall x \in X, \quad \exists y \leq \epsilon
|
|
Srećom, postoji alat koji može dosta olakšati pretragu komandi, za specifične simbole. Tražite "Detexify" u odeljku spoljni linkovi ispod.
Grčka slova
[uredi]Grčka slova se često koriste u matematici, i veoma se lako kucaju u “matematičkom modu”. Samo treba ukucati ime slova posle kose crte: ako je prvo slovo malo, dobićete malo grčko slovo, ako je prvo slovo veliko (i samo prvo slovo), dobićete veliko slovo. Primetite da neka velika grčka slova izgledaju kao latinična, otdua, nije iz obezbedio LaTeX (npr. velika Alpha i Beta su samo "A" i "B"). Mala slova epsilon, teta, kapa, fi, pi, ro, i sigma su obezebeđena preko dve različite verzije. Alternativna, ili '”'variant”, verzija se pravi dodavanjem "var" pre imena slova:
\alpha, \Alpha, \beta, \Beta, \gamma, \Gamma, \pi, \Pi, \phi, \varphi, \Phi
|
|
Operatori
[uredi]Operator je funkcija koja je zapisana kao reč: npr. trigonometrijske funkcije (sin, cos, tan), logaritmi i eksponencijalne (log, exp), limesi (lim), kao i determinante (det). LaTeX ima dosta takvih, definisanih kao komande:
\cos (2\theta) = \cos^2 \theta - \sin^2 \theta
|
|
Za odeđene operatore kao što su granične vrednosti, oznaka se nalazi ispod operatora:
\lim_{x \to \infty} \exp(-x) = 0
|
|
Za modularne operatore postoje dve komande: \bmod i \pmod:
a \bmod b
|
|
x \equiv a \pmod b
|
|
Stepen i indeks
[uredi]Stepeni i indeksi su ekvivalentni superskriptovima i sabskriptovima u normalnom tekst modu. Znak za umetanje (^) karaktera se koristi za podizanje nečega, i donja crta (_) je za spuštanje. Ako je više od jednog izraza podignut ili spušten, oni bi trebalo da budu grupisani koristeći vitičaste zagrade ({ and }).
k_{n+1} = n^2 + k_n^2 - k_{n-1}
|
|
Za stepene, koji imaju više od jedne cifre, okružite stepen {}.
n^{22}
|
|
Donja crta (_) može biti korišćen sa vertikalnom trakom () da označi evaluaciju koristeći sabskript zapis u matematici:
f(n) = n^5 + 4n^2 + 2 |_{n=17}
|
|
Razlomci i binomi
[uredi]Razlomak se pravi \frac{numerator}{denominator} komandom. (da potsetim, to su redom vrh(brojilac) i dno(imenilac)!). Isto tako, binomni koeficijent može biti zapisan korišćenjem: \binom command[3]:
\frac{n!}{k!(n-k)!} = \binom{n}{k}
|
|
Takođe, moguće je koristiti \choose komandu bez amsmath paketa:
\frac{n!}{k!(n-k)!} = {n \choose k}
|
|
Možete ugraditi razlomke, unutar razlomaka:
\frac{\frac{1}{x}+\frac{1}{y}}{y-z}
|
|
Primetiti da, kada se pojavljuje unutar drugog razlomka ili u redu nekog teksta , razlomak je znatno manji nego kada se piše u matematici. \tfrac i \dfrac komande[3] forsiraju korišćenje odgovarajućih stilova, \textstyle ili \displaystyle. Slično, \tbinom i \dbinom komande pišu binomne koeficijente.
Drugi način za pisanje razlomaka jeste korišćenjem \over komande bez amsmath paketa:
{n! \over k!(n-k)!} = {n \choose k}
|
|
Za relativno jednostavne razlomke, posebno unutar teksta, možda bude estetski bolje koristiti stepene i indekse:
^3/_7
|
|
Ako izgleda malo “opušteno” (preveliki razmak), uža verzija može biti definisana ubacivanjem negativnog razmaka
%покретање разломака косом цртом – захтева математички мод.
\newcommand*\rfrac[2]{{}^{#1}\!/_{#2}}
\rfrac{3}{7}
|
|
Ako planirate da ga koristite kroz ceo dokument, preporučuje se xfrac paket.
Paket obezbeđuje \sfrac komandu, da stvori kose razlomke. Upotreba:
Узмите $\sfrac{1}{2}$ шоље шећера, \dots
3\times\sfrac{1}{2}=1\sfrac{1}{2}
Узмите ${}^1/_2$ шоље шећера, \dots
3\times{}^1/_2=1{}^1/_2
|
Ako se razlomci koriste kao eksponente, vitičaste zagrade moraju biti korišćene oko \sfrac komande:
$x^\frac{1}{2}$ % нема грешке
$x^\sfrac{1}{2}$ % грешка
$x^{\sfrac{1}{2}}$ % нема грешке
$x^\frac{1}{2}$ % no error
|
|
U nekim slučajevima, korišćenje samo paketa rezultiraće greškama o određenim nedostupnim oblicima fontova. U tom slučaju, lmodern i fix-cm paketi moraju biti takođe ubačeni.
Alternativno, nicefrac paket obezbeđuje \nicefrac komandu, koja se koristi slično kao i \sfrac.
Kontinuirani razlomci
[uredi]Kontinuirane razlomke treba pisati korišćenjem \cfrac komande[3]:
\begin{equation}
x = a_0 + \cfrac{1}{a_1
+ \cfrac{1}{a_2
+ \cfrac{1}{a_3 + \cfrac{1}{a_4} } } }
\end{equation}
|
|
Množenje dva broja
[uredi]Da bi množenje napravili vizuelno sličnim razlomku, ugnježdeni niz može biti korišćen, na primer, množenje brojeva napisanih jedan ispod drugog.
\begin{equation}
\frac{
\begin{array}[b]{r}
\left( x_1 x_2 \right)\\
\times \left( x'_1 x'_2 \right)
\end{array}
}{
\left( y_1y_2y_3y_4 \right)
}
\end{equation}
|
|
Koren
[uredi]\sqrt komanda pravi kvadratni koren, koji okružuje izraz. Prihvata opcioni argument, koji je specifikovan u uglastim zagradama ([ i ]), kako bi promenio veličinu:
\sqrt{\frac{a}{b}}
|
|
\sqrt[n]{1+x+x^2+x^3+\ldots}
|
|
Neki ljudi vole pisanje kvadratnog korena zatvaranjem istog preko njegovog sadržaja. Ovaj metod čini jasnijim ono što se nalazi u prostoru korenskog znaka. Ova navika se ne koristi često kada pišemo preko kompjutera, ali ako još uvek hoćete da promenite izlaz kvadratnog korena, LaTeX Vam daje tu mogućnost. Samo dodajte sledeći kod u uvodu vašeg dokumenta:
Ovaj TeX kod prvo preimenuje \sqrt komandu kao \oldsqrt, onda ponovo definiše \sqrt u uslovima starog, dodavanjem nečega više. Novi kvadratni koren se može videti na slici na levoj, u poređenju sa starim na desnoj strani. Nažalost, ovaj kod neće raditi ako želite višestruke korenove: ako pokušate da napišete kao \sqrt[b]{a}} \LetLtxMacro{\oldsqrt}{\sqrt} \renewcommand*{\sqrt}[2][\ ]{\oldsqrt[#1]{#2} } \makeatother $\sqrt[a]{b} \quad \oldsqrt[a]{b}$
Međutim, ovo zahteva \usepackage{letltxmacro} paket
Sume i integrali
[uredi]\sum i \int komande redom ubacuju sumu i integral, sa granicama obeleženim karetom (^) i donjom crtom (_). Tipične notacije za sumu su:
\sum_{i=1}^{10} t_i
|
|
ili
\displaystyle\sum_{i=1}^{10} t_i
|
|
Granice integrala se pišu po istom principu. Takođe je bitno pretstaviti integracione promenjive uspravnim “d”, što se, u matematičkom modu, održava kroz \mathrm{} komandu, i odvojiti je malim razlomkom od ostatka integrala, što se postiže \, komandom.
\int_0^\infty \mathrm{e}^{-x}\,\mathrm{d}x
|
|
Postoje i druge "velike" komande koje funkcionišu na sličan način:
\sum |
\prod |
\coprod |
|||||
\bigoplus |
\bigotimes |
\bigodot |
|||||
\bigcup |
\bigcap |
\biguplus |
|||||
\bigsqcup |
\bigvee |
\bigwedge |
|||||
\int |
\oint |
\iint[3] |
|||||
\iiint[3] |
\iiiint[3] |
\idotsint[3] |
Za više integracionih simbola, uključujući i one koji nisu sadžane uobičajnim kompjuter modernim fontom, probajte esint paket.
\substack komanda[3] dozvoljava korišćenje \\, za pisanje granica u više redova:
\sum_{\substack{
0<i<m \\
0<j<n
}}
P(i,j)
|
|
Ako želite da granice integrala budu konkretno iznad i ispod simbola (kao kod sume), koristite \limits komandu:
\int\limits_a^b
|
|
Međutim, ako želite da ovo radi za SVE integraleHowever, poželjno je da specifikujete intlimits opciju, pri učitavanju amsmath paketa:
\usepackage[intlimits]{amsmath}
|
Za veće integrale, možete korstiti lične deklaracije, ili bigints paket [4].
Zagrade
[uredi]Kako koristiti zagrade u jednačinama, koje se prostiru u više redova, opisano je LaTeX/Naprednija matematika poglavlju.
Upotreba graničnika, kao što su zagdare, postaje bitna kada se suočavate sa bilo čim, pa čak i trivijalnim jednačinama. Bez njih, formule mogu postati dvosmislene. Takođe, posebni tipovi matematičkih struktura, kakve su matrice, tipično se oslanjaju na graničnike, koji bi ih zatvorili.
Postoji veliki izbor dostupnih graničnika u LaTeXu:
( a ), [ b ], \{ c \}, | d |, \| e \|,
\langle f \rangle, \lfloor g \rfloor,
\lceil h \rceil, \ulcorner i \urcorner
|
|
gde se \lbrack i \rbrack mogu koristiti umesto [ and ].
Automatsko dimenzionisanje
[uredi]Veoma često će se, matematičke osobine, razlikovati u veličini, u tom slučaju, graničnici, koji okružuju izraz, treba adekvatno da variraju. Ovo se može automatski postići korišćenjem \left, \right, i \middle komandi. Bilo koji, od prethodnih graničnika, se mogu koristiti u kombinaciji sa ovim:
\left(\frac{x^2}{y^3}\right)
|
|
P\left(A=2\middle|\frac{A^2}{B}>4\right)
|
Vitičaste zagrade se različito definišu korišćenjem \left\{ i \right\},
\left\{\frac{x^2}{y^3}\right\}
|
|
Ako je graničnik potreban samo na jednoj strani izraza, onda se nevidljivi graničnik na drugoj strani može napisati korišćenjem perioda (.).
\left.\frac{x^3}{3}\right|_0^1
|
|
Ručno dimenzionisanje
[uredi]U određenim situacijama, dimenzionisanje odrađeno od \left i \right komandi, može da ne bude poželjno, ili možete, jednostavno, želeti finiju kontrolu graničnih veličina. U tom slučaju, \big, \Big, \bigg i \Bigg modifikatorske komande mogu biti korišćene:
( \big( \Big( \bigg( \Bigg(
|
|
Ove komande se primarno korisne kada se suočavate sa ugnežđenim graničnicima. Na primer, za vreme pisanja
\frac{\mathrm d}{\mathrm d x} \left( k g(x) \right)
|
|
primetimo da \left i \right komande daju iste graničnike kao i oni ugnežđeni. Da bismo ovo popravili, pišemo
\frac{\mathrm d}{\mathrm d x} \big( k g(x) \big)
|
|
Ručno dimenzionisanje može, takođe, biti korisno kada je jednačina prevelika, proteže se do kraja stranice, i mora se podeliti u dva reda korišćenjem usklađene komande. Iako, komande \left. i \right. mogu biti korišćene za balanciranje graničnika u svakom redu, ovo može dovesti do pogrešnih gričnih veličina. Štaviše, ručno dimenzionisanje može biti korišćeno za izbegavanje previše velikih graničnika ako se \underbrace ili slična komanda pojavi između graničnika.
Kucanje intervala
[uredi]Za označavanje otvorenih i polu otvorenih intervala, koriste se oznake ]a,b[, (a,b), ]a,b], (a,b], [a,b[ i [a,b). Ako se koristi uglasta zagrada, onda se interval mora staviti između vitičastih zagrada ({ and }), kako bi imali tačan razmak. Slično, ako (polu)otvoren interval počinje negativnim brojem, onda taj broj, uključujući i znak “minus” mora biti stavljen u vitičaste zagrade, tako da LaTeX razume da je “minus” simbol unarna operacija. Uporedite:
x \in [-1,1]
|
|
x \in {[-1,1]}
|
|
x \in {[{-1},1]}
|
|
Matrice i nizovi
[uredi]Osnovna matrica može biti kreirana koristeći matrix okruženje[3]: zajedno sa drugim tabličnim strukturamain, ulazi se specifikuju redom, sa kolonama odvojenim korišćenjem ampersenda (&) i novim redovima, odvojenim duplom kosom crtom (\\)
\begin{matrix}
a & b & c \\
d & e & f \\
g & h & i
\end{matrix}
|
|
Da biste namestili poravnanje kolona u tabeli, koristite verziju sa zvezdicom[5]:
\begin{matrix}
-1 & 3 \\
2 & -4
\end{matrix}
=
\begin{matrix*}[r]
-1 & 3 \\
2 & -4
\end{matrix*}
|
|
Poravnanje po “difoltu” je c, ali može biti bilo koji validan tip kolone u array okruženju.
Međutim, matrice su obično zatvorene u graničnicima neke vrste, i dok je moguće koristiti \left i \right commands, postoje mnogobrojna druga definisana okruženja, koja automatski uključuju graničnike:
| Ime okljuženja | Zagrade koje okružuju | Beležke |
|---|---|---|
| pmatrix[3] | centrira kolone po “difoltu” | |
| pmatrix*[5] | omogućava da odredite poravnanje kolona u opcionim parametrima | |
| bmatrix[3] | centrira kolone po “difoltu” | |
| bmatrix*[5] | omogućava da odredite poravnanje kolona u opcionim parametrima | |
| Bmatrix[3] | centrira kolone po “difoltu” | |
| Bmatrix*[5] | omogućava da odredite poravnanje kolona u opcionim parametrima | |
| vmatrix[3] | centrira kolone po “difoltu” | |
| vmatrix*[5] | omogućava da odredite poravnanje kolona u opcionim parametrima | |
| Vmatrix[3] | centrira kolone po “difoltu” | |
| Vmatrix*[5] | omogućava da odredite poravnanje kolona u opcionim parametrima |
Za vreme pisanja matrica proizvoljnih veličina, uobičajno je koristiti horizontalne, vertikalne i dijagonalne triplete tačaka, kako bi ispunili određene kolone i redove. Ovo se može specifikovati korišćenjem redom \cdots, \vdots i \ddots:
A_{m,n} =
\begin{pmatrix}
a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\
a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m,1} & a_{m,2} & \cdots & a_{m,n}
\end{pmatrix}
|
|
U nekim situacijama, možda ćete želeti finiju kontrolu ravnanja unutar svake kolone, ili možda želeti da ubacite redove između kolona ili redova. Ovo se može postići korišćenjen array okruženja, što je, suštinski, matematička verzija tabular environment, koje zahteva da kolone budu prethodno navedene:
\begin{array}{c|c}
1 & 2 \\
\hline
3 & 4
\end{array}
|
|
Možete videti da AMS matrična klasa okruženja ne ostavlja dovoljno prostora, kada se koristi istovremeno sa razlomcima, rezultirajući izlaz sličan ovome:
Da biste kontrirali ovom problemu, ubacite dodatni prostor sa opcionim parametrom u \\ komandu:
M = \begin{bmatrix}
\frac{5}{6} & \frac{1}{6} & 0 \\[0.3em]
\frac{5}{6} & 0 & \frac{1}{6} \\[0.3em]
0 & \frac{5}{6} & \frac{1}{6}
\end{bmatrix}
|
|
Ako vam zatrebaju "granice" ili "indeksi" u matrici, osnovni TeX obezbeđuje makro \bordermatrix
M = \bordermatrix{~ & x & y \cr
A & 1 & 0 \cr
B & 0 & 1 \cr}
|
Matrice u tekstu
[uredi]Kako biste ubacili malo matricu, a da pritom ne povećate red koji je sadrži, koristite smallmatrix okruženje:
Матрица у тексту мора бити мања:
$\bigl(\begin{smallmatrix}
a&b \\ c&d
\end{smallmatrix} \bigr)$
како не би повећала текст.
|
Rendering missing! |
Dodavanje teksta u jednačinama
[uredi]Matematičko okruženje se razlikuje od tekstualnog u predstavljanju teksta. Evo primera za pokušaj prikazivanja teksta unutar matematičkog okruženja:
50 јабука \times 100 јабука = доста јабука^2
|
|
Postoje dva primetna problema: nema razmaka između reči ili brojeva, i slova su u “italik” fontu i sa većim razmakom nego obično. Oba problema su, jednostavno, artefakti matematičkog moda, u kojem se ophodi prema njima kao matematičkim iskazima: razmaci su ignorisani (LaTeX stavlja razmake u matematici po svojim pravilima), i svaki karakter je odvojen element (tako da nisu pozicionirani toliko blisko kao u normalnom tekstu).
Postoji više načina za tačno dodavanje teksta. Tipičan način jeste “zamotavanje” teksta \text{...} komandom [3] (slična komanda je \mbox{...}, premda ovo stvara probleme sa sabskriptom, i ima manje opisno ime). Da vidimo šta se događa kada je gornja jednačina adaptirana:
50 \text{јабука} \times 100 \text{јабука}
= \text{доста јабука}^2
|
|
Tekst izgleda bolje. Međutim, nema praznina između brojeva i slova. Nažalost, dužni ste da ih eksplicitno dodate. Postoji dosta načina za dodavanje razmaka između matematičkih elemenata, ali zbog jednostavnosti možemo samo dodati razmak u \text komandu.
50 \text{ јабука} \times 100 \text{ јабука}
= \text{доста јабука}^2
|
|
Formatiran tekst
[uredi]Korišćenje \text je u redu i daje osnovni rezultat. Ipak, postoji alternativa koja daje veću fleksibilnost. Možete se vratiti na uvod komandi za formatiranje fontova, kao što su \textrm, \textit, \textbf, itd. Ove komande tačno formatiraju argumente, npr., \textbf{bold text} daje boldirani tekst. Ove komande su jednako validne unutar matematičkog okruženja, kada je u pitanju ubacivanje teksta. Prednost ovoga jeste u tome što možete imati bolju kontrolu oko formatiranja fontova (slova), više nego u standardnom tekstu unutar \text.
50 \textrm{ јабука} \times 100
\textbf{ јабука} = \textit{доста јабука}^2
|
|
Formatiranje matematičkih simbola
[uredi]Sada možemo da formatiramo tekst; ali šta je sa formatiranjem matematičkih izraza? Postoji komplet komandi formatiranja, koji je veoma sličan upravo korišćenom formatiranju fonta, osim što su specifično ciljani na tekst u matematičkom modu (zahtevaju amsfonts)
| LaTeX komanda | Uzorak | Opis | Česta upotreba |
|---|---|---|---|
\mathnormal{…}(ili jednostavno izostaviti bilo koju komandu) |
Običan matematički font | Većina matematičkih notacija | |
\mathrm{…}
|
Ovo je običan ili normalan font, bez “italika” | Merne jedinice, funkcije sačinjene od jedne reči(trigonometrija) | |
\mathit{…}
|
“Italik” font | Funkcije sačinjene od više slova ili imena varijabli. U poređenju sa \mathnormal, reči su odvojene prirodnije i brojevi su, takođe, na “italik” fontu.
| |
\mathbf{…}
|
“Bold” font | Vektori | |
\mathsf{…}
|
Beserifni | ||
\mathtt{…}
|
”Monospejs” font | ||
\mathfrak{…}
|
Fraktur | Skoro kanonski font za algebru, sa supskriptom koja se koristi da označi papire Novog Zaveta, ideala u teoriji prstena. | |
\mathcal{…}
|
Kaligrafija (samo velika slova) | Često se koristi za snopove/šeme i kategorije, koristi se da označi kriptografičke koncepte kao što je alfabet definicija (), prostor poruke (), prostor šifrata () and prostor ključeva (); “Klinovo” ]]; “davanje imena konvencijama u opisnoj logici”; Laplasova transformacija () i Furijeov red () | |
\mathbb{…}(zahteva amsfonts ili amssymb paket) |
”Blekbord” bold (samo velika slova) | Koristi se za označavanje specijalnih kompleta (npr. realnih brojeva) | |
\mathscr{…}(zahteva mathrsfs paket) |
Skripta (samo velika slova) | Alternativni font za kategorije i šeme. |
Evo komande formatiranja mogu “okružiti” čitave jednačine, i to ne samo na tekstualnim elementima: oni samo formatiraju slova, brojeve i velika grčka slova, i ostale matematičke komande su nepromenjene.
Boldirana mala grčka slova ili ostali simboli koriste \boldsymbol komandu[3]; ovo će samo raditi ako postoji “bold” verzija simbola u trenutnom fontu. Kao poslednje utočište postoji \pmb komanda[3] (“bold” siromašnog čoveka): ovo štampa više verzija karaktera koji se malo razlikuju jedan od drugog.
\boldsymbol{\beta} = (\beta_1,\beta_2,\dotsc,\beta_n)
|
|
Akcenti
[uredi]Šta raditi kada ostanete bez simbola i fontova? Sledeći korak je koišćenje akcenata:
a' or a^{\prime} |
a'' |
||
\hat{a} |
\bar{a} |
||
\grave{a} |
\acute{a} |
||
\dot{a} |
\ddot{a} |
||
\not{a} |
\mathring{a} |
||
\overrightarrow{AB} |
\overleftarrow{AB} |
||
a''' |
a'''' |
||
\overline{aaa} |
\check{a} |
||
\breve{a} |
\vec{a} |
||
\dddot{a}[3] |
\ddddot{a}[3] |
||
\widehat{AAA} |
\widetilde{AAA} |
||
\widehat{AAA} |
\stackrel\frown{AAA} |
||
\tilde{a} |
\underline{a} |
Boja
[uredi]Paket xcolor, opisan u Boje, dozvoljava nam dodavanje boje našoj jednačini. Na primer,
k = {\color{red}x} \mathbin{\color{blue}-} 2
|
|
Jedini problem je što ovo remeti uobičajno LaTeX formatiranje oko - operatora. Da bi popravili ovo, mi ga ograđujemo u \mathbin okruženju, pošto je - binarna operacija. Ovaj proces je opisan ovde.
Plus i minus znaci
[uredi]LaTeX se nosi sa + i − znacima na dva moguća načina. Najučestaliji je binarni operator. Kada se dva matematička elementa pojave na bilo kojoj strani znaka, pretpostavlja se da je u pitanju binarna operacija, i kao takva, dodeljuje razmak na obe strane znaka. Alternativni način je imenovanje znaka. Ovo je kada označavate da li je matematička jednakost pozitivna ili negativna. Ovo je uobičajno za ono drugo, pošto u matematici, svi elementi se računaju kao pozitivni, osim ako nemaju − prefiks ispred. U ovom slučaju, želite da se znak pojavi blizu odgovarajućeg elementa, kako bi pokazao njihovu povezanost. Ako stavite + ili − bez ičega pre njega, ali želite da se njim barata kao binarnom operacijom, možete dodati “nevidljiv” karakter pre operatora koristeći {}. Ovo može biti korisno ako pišete formule u nekoliko redova, a novi red počinje sa = ili +, na primer, onda možete popraviti neobična poravnanja dodavajući nevidljivi karakter tamo gde je to potrebno.
Plus-minus znak se piše kao:
\pm
|
|
Slično tome, takođe, postoji minus-plus znak:
\mp
|
|
Kontrola horizontalnog razmaka
[uredi]LaTeX je, očigledno, veoma dobar u pisanju matematike—to je bio jedan od glavnih ciljeva jezgra TeX sistema koji LaTeX produžuje. Međutim, ne može se uvek na njega osloniti da jasno interpretira formule, na način na koji ste Vi to uradili. Mora da napravi određene pretpostavke kada ima dvosmislenih izraza. Rezultat može biti nekorektan u smislu horizontalnog razmaka. U tim slučajevima, izlaz je još uvek zadovoljavajući, ipak perfekcionisti će, bez sumnje, želeti da fino podese svoje formule, kako bi osigurali pravilne horizontalne razmake. Ovo su, generalno, veoma suptilna prilagođavanja.
Postoje drugi slučajevi, gde je LaTeX korektno obavio svoj posao, ali samo želite da dodate malo razmaka, možda dodate komentar neki. Na primer, u sledećoj jednačini, poželjno je osigurati da postoji određen razmak između matematike i teksta.
\[ f(n) =
\begin{cases}
n/2 & \quad \text{if } n \text{ is even}\\
-(n+1)/2 & \quad \text{if } n \text{ is odd}\\
\end{cases}
\]
|
|
Ovaj kod izbacuje grešku ako koristite Miktex 2.9 i ne izbacuje rezultat, koji je viđen kao tačan. Koristite \mathrm umesto samo \text.
(Primetiti da konkretno ovaj primer može biti izražen elegantnijim kodom korišćenjem cases okruženja, obezbeđenog od amsmath paketa opisanog u poglavlju Naprednija matematika.)
LaTeX je definisao dve komande koje mogu biti korišćene za ubacivanje horizontalnog razmaka bilo gde u dokumentu (ne samo u matematici). To su \quad i \qquad
\quad je razmak jednak veličini fonta. Dakle, ako koristite “11pt” font, onda će razmak, obezbeđen od \quad, takođe biti “11pt” (naravno, horizontalno). \qquad daje duplo veći razmak od fonta. Kao što možete videti iz koda, u prethodnom primeru, \quad-ovi su korišćeni za dodavanje razmaka između matematike i teksta.
Dakle, vraćamo se na fino podešavanje pomenuto na početku dokumenta. Dobar primer bi bio pokazivanje jednostavne jednačine nedefinisanog integrala.
Ako ćete ovo pokušati, možete i napisati:
\int y \mathrm{d}x
|
|
Međutim, ovo ne daje korektan rezultat. LaTeX ne poštuje razmak ostavljen u kodu koji označava da su y i dx nezavisni entiteti. Umesto toga, on ih spaja sve zajedno. \quad bi, očigledno, bio “pretučen” u ovoj situaciji—ono što je potrebno jesu mali razmaci koji će biti korišćeni u ovakvom primeru, i to je ono što LaTeX pruža:
| Komanda | Opis | Veličina |
|---|---|---|
\,
|
mali razmak | 3/18 “quad”-a |
\:
|
srednji razmak | 4/18 “quad”-a |
\;
|
veliki razmak | 5/18 “quad”-a |
\!
|
negativni razmak | -3/18 “quad”-a |
Napomena: možete koristiti više od jedne komande ukoliko Vam je potreban veći razmak.
Dakle, da ispravimo trenutni problem:
\int y\, \mathrm{d}x
|
|
\int y\: \mathrm{d}x
|
|
\int y\; \mathrm{d}x
|
|
Negativni razmak možda deluje kao čudna stvar za korišćenje, međutim, ne bi bilo tu da od njega nema “neke” koristi! Uzmite sledeći primer:
\left(
\begin{array}{c}
n \\
r
\end{array}
\right) = \frac{n!}{r!(n-r)!}
|
|
Matrični iskaz za prikazivanje binomnih koeficijenata je previše tapaciran. Previliki je razmak između zagrade i saržaja unutar istih. Ovo se lako može ispraviti dodavanjem par negativnih razmaka, posle leve i pre desne zagrade.
\left(\!
\begin{array}{c}
n \\
r
\end{array}
\!\right) = \frac{n!}{r!(n-r)!}
|
|
U svakom slučaju, ručno dodavanje razmaka treba izbegavati kad god je to moguće: to čini izvorni kod kompleksnijim i u suprotnosti je sa osnovnim principom “To što vidiš je ono na šta si mislio” pristupa. Najbolja stvar za činiti jeste definisanje nekih komandi koristeći sve razmake koje želite i onda, kada koristite svoju komandu, ne treba da dodajete više razmake. Kasnije, ako se predomislite kada je u pitanju dužina horizonalnog razmaka, lako ga možete promeniti, modifikovanjem komande koju ste ranije definisali. Hajde da ovo pokažemo na primeru: ako želite d od dx u integralu da bude u rimskom fontu i malo razdvojeno od ostatka. Ako želite da napišete ovakav integral \int x \, \mathrm{d} x, možete definisati ovakvu komandu:
\newcommand{\dd}{\mathop{}\,\mathrm{d}}
|
u uvodu vašeg dokumenta. Izavrali smo \dd samo zato što potseća da je "d" zamenjeno i zato što je brzo za kucanje. Na taj način, kod Vašeg integrala postaje \int x \dd x. Sada, kada god pišete integral, samo morate da koristite \dd umesto "d", i svi Vaši integrali će imati isti stil. Ako se predomislite, samo treba da promenite definiciju u uvodu, i svi Vaši integrali će se promeniti po definiciji.
Ručno određivanje stila formule
[uredi]Da ručno prikažete fragment formule koristeći tesktualni stil, okružite fragment vitičastim zagradama i stavite prefiks fragmentu uz pomoć \textstyle. Zagrade su obavezne zbog \textstyle makro menja stanje prikazivača, prikazivajući sve ostale delove matematike u tekstualnom stilu. Zagrade limitiraju promenu stanja na samo fragment u istim. Na primer, za korišćenje tekstualnog stila samo za zbir simbola u sumi, uneli biste
\begin{equation}
C^i_j = {\textstyle \sum_k} A^i_k B^k_j
\end{equation}
|
Ista stvar, ali kao komanda, izgledala bi ovako:
\newcommand{\tsum}[1]{{\textstyle \sum_{#1}}}
|
Primetite dodatne zagrade. Samo jedan par oko izraza neće biti dovoljan. To bi izazvalo da svaka kasnija matematika \tsum k bude prikazana korišćenjem tekstualnog stila.
Da prikažete deo formule, korišćenjem prikazivačkog stila, uradite istu stvar, ali koristite \displaystyle.
Naprednija matematika: “AMS Math” paket
[uredi]“AMS” (“American Mathematical Society”) matematički paket jeste moćan paket koji pravi viši sloj apstrakcija u matematičkom LaTeX jeziku; ako ga koristite, olakšaće Vam život. Neke uvedene komande amsmath paketa će učini da druge osnovne LaTeX komande deluju zastarelo: kako biste održavali konstantnost u finalnom izlazu, bolje bi bilo da koristite amsmath komande, kad god je to moguće. Ako tako učinite, dobićete elegantan izlaz bez brige o poravnanju i drugim detaljima, čineći izvorni kod čitkim. Ako želite da ga korisistite, u uvod morate ovo da ubacite:
\usepackage{amsmath}
|
Uvođenje tačaka u formule
[uredi]amsmath definiše takođe \dots komandu, što je generalizacija već postojeće \ldots. Možete koristiti \dots i u tekstualnom i matematičkom modu i LaTeX će je zameniti sa tri tačke "…" , ali će odlučiti na osnovu konteksta da li da ga stavi na dnu kao (kao \ldots) ili centirano (kao \cdots).
Tačke
[uredi]LaTeX daje nekoliko komandi za ubacivanje tačaka (elipsi) u Vašu formulu. Ovo može biti posebno korisno ako pišete velike matrice i izbegavate elemente. Pre svega, evo osnovni komandi vezanih za tačke koje LaTeX obezbeđuje:
| Kod | Izlaz | Komentar |
|---|---|---|
\dots |
opšte tačke , korišćene u tekstu (takođe, izvan formule). Automatski sređuje razmake pre i posle sebe, po kontekstu, to je komanda višeg reda. | |
\ldots |
izlaz je sličan prethodnom, ali nema automatskog sređivanja razmaka; radi na nižem nivou. | |
\cdots |
Tačke su centrirane relativno u odnosu na visinu slova. Takođe, postoji binarni operator množenja, \cdot, pomenut ispod.
| |
\vdots |
Vertikalne tačke. | |
\ddots |
Dijagonalne tačke. | |
\iddots |
Inverzne dijagonalne tačke (zahtevaju mathdots paket). | |
\hdotsfor{n} |
Koriste se u matricama, pravi red tačaka koje se šire kroz n kolona. |
Umesto korišćenja \ldots i \cdots, treba da koristite semantički orijentisane komande. Time postaje moguće, u letu, adaptirati svoj dokument drugačijim konvencijama, u slčaju (na primer) da ,prate da pošaljete izdavaču koji insistira na praćenju “kućne” tradicije. Uobičajni tretman za različite vrste prati konvencije Američkog društva matematičara.
Lista matematičkih simbola
[uredi]Svi definisani matematički simboli iz \TeX\ paketa nabrojani su ispod. Još simbola je dostupno iz dodatnih paketa.
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
<
|
>
|
=
|
\parallel
|
\nparallel
| |||||||||
\leq
|
\geq
|
\doteq
|
\asymp
|
\bowtie
| |||||||||
\ll
|
\gg
|
\equiv
|
\vdash
|
\dashv
| |||||||||
\subset
|
\supset
|
\approx
|
\in
|
\ni
| |||||||||
\subseteq
|
\supseteq
|
\cong
|
\smile
|
\frown
| |||||||||
\nsubseteq
|
\nsupseteq
|
\simeq
|
\models
|
\notin
| |||||||||
\sqsubset
|
\sqsupset
|
\sim
|
\perp
|
\mid
| |||||||||
\sqsubseteq
|
\sqsupseteq
|
\propto
|
\prec
|
\succ
| |||||||||
\preceq
|
\succeq
|
\neq
|
\sphericalangle
|
\measuredangle
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | |||
|---|---|---|---|---|---|---|---|---|---|---|
\pm
|
\cap
|
\diamond
|
\oplus
| |||||||
\mp
|
\cup
|
\bigtriangleup
|
\ominus
| |||||||
\times
|
\uplus
|
\bigtriangledown
|
\otimes
| |||||||
\div
|
\sqcap
|
\triangleleft
|
\oslash
| |||||||
\ast
|
\sqcup
|
\triangleright
|
\odot
| |||||||
\star
|
\vee
|
\bigcirc
|
\circ
| |||||||
\dagger
|
\wedge
|
\bullet
|
\setminus
| |||||||
\ddagger
|
\cdot
|
\wr
|
\amalg
|
| Symbol | Script | Symbol | Script | |
|---|---|---|---|---|
\exists
|
\rightarrow or \to
| |||
\nexists
|
\leftarrow or \gets
| |||
\forall
|
\mapsto
| |||
\neg
|
\implies
| |||
\subset
|
\Rightarrow or \implies
| |||
\supset
|
\leftrightarrow
| |||
\in
|
\iff
| |||
\notin
|
\Leftrightarrow (preferred for equivalence (iff))
| |||
\ni
|
\top
| |||
\land
|
\bot
| |||
\lor
|
and | \emptyset and \varnothing
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | |||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
\|
|
/
|
\backslash
| |||||||
\{
|
\}
|
\langle
|
\rangle
| |||||||
\uparrow
|
\Uparrow
|
\lceil
|
\rceil
| |||||||
\downarrow
|
\Downarrow
|
\lfloor
|
\rfloor
|
Beleška: Za korišćenje grčkih slova u LaTeXu, koja imaju isti izgled kao njihovi rimski ekvivalenti, samo koristite rimsku formu: e.g., “A” umesto “Alpha”, “B” umesto “Beta”, itd.
| Symbol | Script | Symbol | Script | |
|---|---|---|---|---|
| and | A and \alpha
|
and | N and \nu
| |
| and | B and \beta
|
and | \Xi and \xi
| |
| and | \Gamma and \gamma
|
and | O and o
| |
| and | \Delta and \delta
|
, and | \Pi, \pi and \varpi
| |
| , and | E, \epsilon and \varepsilon
|
, and | P, \rho and \varrho
| |
| and | Z and \zeta
|
, and | \Sigma, \sigma and \varsigma
| |
| and | H and \eta
|
and | T and \tau
| |
| , and | \Theta, \theta and \vartheta
|
and | \Upsilon and \upsilon
| |
| and | I and \iota
|
, , and | \Phi, \phi and \varphi
| |
| , and | K, \kappa and \varkappa
|
and | X and \chi
| |
| and | \Lambda and \lambda
|
and | \Psi and \psi
| |
| and | M and \mu
|
and | \Omega and \omega
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
\partial
|
\imath
|
\Re
|
\nabla
|
\aleph
| |||||||||
\eth
|
\jmath
|
\Im
|
\Box
|
\beth
| |||||||||
\hbar
|
\ell
|
\wp
|
\infty
|
\gimel
|
| Symbol | Script | Symbol | Script | Symbol | Script | Symbol | Script | |||
|---|---|---|---|---|---|---|---|---|---|---|
\sin
|
\arcsin
|
\sinh
|
\sec
| |||||||
\cos
|
\arccos
|
\cosh
|
\csc
| |||||||
\tan
|
\arctan
|
\tanh
|
||||||||
\cot
|
\arccot
|
\coth
|
Rezime
[uredi]Kao što možete videti, kucanje matematike može biti ponekad teško. Međutim, jer LaTeX nudi toliko kontrole, možete dobiti veoma profesionalno otkucanu matematiku sa relativno malo truda (kada uđete u štos, naravno!). Bilo bi moguće nastaviti sa temom matematike, jer deluje kao da nema kraj. Međutim, ovim “tutorijalom”, trebalo bi brzo da uhvatite priključak.
Beleške
[uredi]- ↑ http://www.ams.org/publications/authors/tex/amslatex
- ↑ http://www.ctan.org/tex-archive/macros/latex/contrib/mathtools/mathtools.pdf
- ↑ 3,00 3,01 3,02 3,03 3,04 3,05 3,06 3,07 3,08 3,09 3,10 3,11 3,12 3,13 3,14 3,15 3,16 3,17 3,18 requires the amsmath package
- ↑ http://hdl.handle.net/2268/6219
- ↑ 5,0 5,1 5,2 5,3 5,4 5,5 requires the mathtools package
Spoljni linkovi
[uredi]- LaTeX maths symbols
- detexify: applet for looking up LaTeX symbols by drawing them
- amsmath documentation
- LaTeX - The Student Room
- The Comprehensive LaTeX Symbol List
- MathLex - LaTeX math translator and equation builder

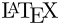























![{\displaystyle {\sqrt[{n}]{1+x+x^{2}+x^{3}+\ldots }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c20a0cedb6864fce2fb1395a58699288b7a507b0)

![{\displaystyle {\sqrt[{b}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ceeccbbf1609652afdb8d84d33552cd2731bb0d)























![{\displaystyle (a),[b],\{c\},|d|,\|e\|,\langle f\rangle ,\lfloor g\rfloor ,\lceil h\rceil ,\ulcorner i\urcorner }](https://wikimedia.org/api/rest_v1/media/math/render/svg/61234d9b478821fe1f357388b1f4f098e5745b81)






![{\displaystyle x\in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722)
![{\displaystyle x\in {[-1,1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a18934c1ca2e4c5a3b42159017fb6fef2e3d9b4b)
![{\displaystyle x\in {[{-1},1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15fe4946dcbe93e3bf8fca8fa5d70bb39da0eee2)



![{\displaystyle [\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5444b5227fcebf7e7cbb9ee114af1373f6a2e95)






![{\displaystyle M={\begin{bmatrix}{\frac {5}{6}}&{\frac {1}{6}}&0\\[0.3em]{\frac {5}{6}}&0&{\frac {1}{6}}\\[0.3em]0&{\frac {5}{6}}&{\frac {1}{6}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4989d4433782a036095cdf274ee636c5f783125c)































































































































































































































































