Algoritmi/Dinamičko programiranje
Dinamičko programiranje se može posmatrati kao optimizaciona tehnikaza određene klase bektreking algoritama gde se pod problemi u više navrata rešavaju. Primetite da se izraz dinamičko u dinamičkom programiranju ne sme mešati dinamičkim jezicima za programianje, kao što su Scheme ili Lisp. Niti bi termin programiranje smeo da se meša sa činom pisanja kumpjuterskih programa. U kontekstu algoritama, dinamičko programiranje se uvek odnosi na tehniku popunjavanja tabele vrednostima koje su izračunate od vrednosti drugih tabela. (ovo je dinamičko jer se vrednosti u tabeli popunjavaju od strane algoritma baziranog na ostalim vrednostima tabele, a programiranje je jer u smislu smeštanja stvari u tabelu, kao na primer, kako se programiranje televizija brine o tome kad će se emitovati koja emisija.)
Fibonačijevi brojevi
[uredi]Pre nego što ćemo predstaviti tehniku dinamičkog programiranja, korisno je da najpre prikažemo srodnu tehniku, koja se zove memorizacija, na primeru Fibonačijevih brojeva. Ono što želimo da napravimo je rutina koja izračunava n-ti Fibonačijev broj:
// fib -- рачуна Fibonacci(n) function fib(integer n): integer
Po definiciji, nti Fibonačijev broj, u oznaci je:
Kako bismo napravili dobar algoritam za nalaženje n-tog Fibonačijevog broja? Počnimo sa naivnim algoritmom, koji kodira matematičku definiciju:
// fib -- рачуна Fibonacci(n) function fib(integer n): integer assert (n >= 0) if n == 0: return 0 fi if n == 1: return 1 fi return fib(n - 1) + fib(n - 2) end
Primetite da je ovo vrlo jednostavan primer jer postoji matematički izraz za izračunavanje :
Gde je:
Ova druga jednačina je poznata kao zlatna razmera Golden Ratio. Naime, program bi mogao efikasno da računa čak i za veoma veliko n. Međutim, bitno je da se razume zbog čeka je ovaj algoritam toliko neefikasan. Kako bismo analizirali vreme potrebno za izvršavanje koda fib , pogledaćemo stablo poziva za nešto tako malo kao što je šesti Fibonačijev broj:
Svaki list iz stabla poziva ima vednost 0 ili 1, i suma ovih vrednosti je konačni rezultat. Tako, za bilo koje n, broj listova u stablu poziva je ustvari . Zatvorena forma na govori da je broj listova u fib(n) približno jednak:
( Uočite algebarsku manipulaciju korišćenu u izrazu iznad kako bi baza eksponenta bila jednaka broju 2.) Ovo znači da ima previše listova, posebno ako se uzmu u obzir ponavljani šabloni koji se nalaze u stablu poziva na slici iznad. Jedna optimizacija koju možemo da napravimo je da sačuvamo rezultat u tabelu kad se izračuna, tako da se jedan isti rezultat računa samo jednom. Optimizacioni proces se zove memorizacija i prilagođen je sledećoj metodologiji:
Metodologija memorizacije
|
Uzeti u obzir rešenje prezentovano u poglavlju bektreking, za problem najduže zajedničke pod sekvence. Tokom izvršavanja tog algoritma, mnogi zajednički pod problemi su izračunavani više puta. Kao optimizaciju, možemo izračunati ove pod probleme jednom, a zatim zapamtiti rezultate da bi se kasnije pročitali. Rekurzivni algoritam sa memorizacijom se može izvrnuti u iterativni algoritam koji popunjava tabelu rešenja pod problema. Neki od rešenih pod problema možda neće biti potrebni za konačno rešenje (ovde se dinamičko programiranje razlikuje od memorizacije), ali dinamičko programiranje može biti veoma efikasno jer njegova iterativna verzija bolje koristi keš memoriju i ima manji višak poziva. Asimptotski, dinamičko programiranje i memorizacija imaju isto komplkesnost. Dakle, kako bi program brojeva radio koristeći memorizaciju? Posmatrajmo sledeći program (f[n] sadrži n-ti Fibonačijev broj ako je on izračunat, u suprotnom, sadrži vrednost -1):
function fib(integer n): integer
if n == 0 or n == 1:
return n
else-if f[n] != -1:
return f[n]
else
f[n] = fib(n - 1) + fib(n - 2)
return f[n]
fi
end
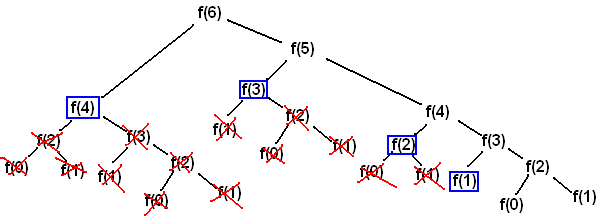
Kod bi trebalo da bude poprilično očigledan. Ako je vrednost fib(n) već izračunata, onda je ona zapamćena u f[n] i zatim vraćena umesto da se ponovo računa. Ovo znači da se sve kopije iz stabala pod poziva uklanjaju iz kalkulacije.
Vrednosti u plavim pravougaonicima su vrednosti koje su već izračunate i pozivi bi onda mogli da se preskoče. Ovaj algoritam je mnogo brži od običnog rekurzivnog algoritma. Kako se svaka vrednost manja od n računa samo jednom, prvi puta kada s epokrene program, asimptotsko vreme izvršavanje koda je . Svaki drugi poziv će imati vreme izvšavanja, jer su vrednosti već izračunate ( pod pretpostavkom da je argument svakog poziva sub sekvence manji od n). Ovaj algoritam koristi mnogo memorije. Kada računamo fib(n), vrednosti fib(0) do fib(n) se skladište u glavnu memoriju. Da li ovo može da se unapredi? Da, može, mada će vreme izvršavanja sub sekvencijalnih poziva da se izgubi jer vrednosti nisu memorisane. Kako vrednost fib(n) zavisi samo od vrednosti fib(n-1) i fib(n-2), ostale vrednosti možemo odbaciti tako što idemo od dna ka vrhu. Ako želimo da izračunamo fib(n), prvo izračunamo fib(2)=fib(0) + fib(1). Zatim računamo fib(3) tako što saberemo fib(1) i fib(2). Posle toga fib(0) i fib(1) mogu da se odbac, jer nam nisu potrebni za računanje novih vrednosti. Od fib(2) i fib(3) računamo fib(4) i odbacujemo fib(2), zatim računamo fib(5) i odbacujemo fib(3), itd. Kod za ovo izgleda ovako:
function fib(integer n): integer
if n == 0 or n == 1:
return n
fi
let u := 0
let v := 1
for i := 2 to n:
let t := u + v
u := v
v := t
repeat
return v
end
Možemo da modifikujemo kod da skladišti vrednosti u niz za pod sekvencijalne pozive, ali poenta je u tome da ne moramo. Ovaj metod je tipičan za dinamičko programiranje. Prvo identifikujemo koji pod problemi treba da se reše kako bi se rešio celokupan problem, a zatim računamo vrednosti od dna ka početku koristeći iterativni proces.
Najduža zajednička pod sekvenca (verzija sa dinamičkim programiranjem)
[uredi]Ovo će nas podsetiti na bektreking verziju, a zatim ćemo je unaprediti uz pomoć memorizacije. Konačno, rekurzivni algoritam će postati iterativan i biće pravo rešenje korišćenjem dinamičkog programiranja.
Lančano množenje matrica
[uredi]Zamislimo da treba da pomnožimo seriju od matrica kako bismo formirali matricu proizvoda :
Ovo će zahtevati množenje, ali koji je najbrži način za dobijanje ovog proizvoda? Množenje matrica je asocijativno, tj.:
Za svako , tako da možemo da biramo koje množenje ćemo prvo da obavimo. ( Primetite da množenje matrica nije komutativno, tj. ne važi .) Kako možemo množiti samo dve matrice u trenutku, proizvod može biti podeljen na sledeće načine:
Dve matrice i mogu da se množe samo ako je broj kolona jedne matrice jednak broju redova druge. Broj redova njihovog proizvoda biće jednak broju redova prve matrice, a broj kolona će biti jednak broju kolona druge matrice. Dakle, ako su dimenzije i ima dimenzije njihov proizvod će imati dimenzije .
Za množenje dve matrice, koristimo funkciju koja se zove množenje matrica, koja uzima dve matrice i vraća njihov proizvod. Za sad nećemo pričati o implementaciji ove funkcije jer to nije cilj ovog poglavlja (kako najbrže pomnožiti dve matrice je problem koji se intenzivno izučava već nekoliko godina). Vreme koje je ovoj funkciji potrebno da pomnoži dve matrice dimenzija i je proporcionalno broju skalarnih množenja, koji je proporcionalan . Tako da je podela proizvoda većeg broja matrica bitna: recimo da imamo, na primer tri matrice , i . ima dimenzije , , ima dimenzije i ima dimenzije . Hajde da podelimo ovaj proizvoda na dva moguća načina i da vidimo koji način zahteva najmanju količinu množenja. Ta dva načina su sledeći:
- , i
- .
Formiranje proizvoda na prvi način zahteva 75000 skalarnih množenja (5*100*100=50000 za formiranje proizvoda i još 5*100*50=25000 za poslednja množenja.) Ovo može da deluje kao veliki broj, ali u poređenju sa 525000 skalarnih množenja koja su potrebna za računanje proivoda na drugi način (50*100*100=500000 plus 5*50*100=25000) je zanemarljivo! Odavde možete videti kako je izbor načina podele proizvoda matrica veoma važan: zamislite šta bi se desilo kad bi trebalo da se izračuna proizvod 50 matrica!
Formiranje rekurzivnog rešenja
[uredi]Uočite da se bavimo nalaženjem broja potrebnih skalarnih množenja, umesto poretka. Ovo je zbog toga što, kad nađemo dobar algoritam za nalaženje količine množenja, kreiranje algoritma za podelu proizvoda postaje trivijalno. Ovo će biti pomenuto na kraju poglavlja. Dakle, kako bi algoritam za optimalnii podelu proizvoda izgledao? Po naslovu poglavlja, da je u pitanju metod dinamičkog programiranja. Dakle kako bi metod dinamičkog programiranja radio? Kako su algoritmi dinamičkog programiranja bazirani na optimalnoj pod strukturi, šta bi bila optimalna pod struktura za ovaj problem? Zamislimo da optimalna podela proizvoda
Deli proizvod kod k-te matrice:
- .
Onda optimalno rešenje sadrži optimalna rešenja za dva pod problema
Ovo je u saglasnosti sa fundamentalnim principom dinamičkog programiranja, rešenje problema zavisi od rešenja problema manjih pod problema. Recimo da je potrebno skalarnih množenja kako bi se pomnožile matrice i , i je broj skalarnih množenja kada se koristi optimalna podela proizvoda matrica . Definisanje je prvi korak ka rešenju. Kada je , formulacija je trivijalna; to je samo . Ali šta je kada je distanca veća? Koristeći observaciju odozgo, možemo da dođemo do formulacije. Pretpostavimo da optimalno rešenje problema deli proizvod kod matrica k i k+1 (na primer, ) onda je broj skalarnih množenja jednak:
To je vreme potrebno za formiranje prvog proizvoda, drugog proizvoda i vreme potrebno za formiranje konačnog proizvoda. Ali koja je ova optimalna vrednost k? Odgovor je, naravno, vrednost za koju formula odozgo ima minimalnu vrednost. Na taj način možemo formirati kompletnu definiciju funkcije:
Rekurzivno rešenje bi izgledalo ovako:
function f(m, n) {
if m == n
return 0
let minCost :=
for k := m to n - 1 {
v := f(m, k) + f(k + 1, n) + c(k)
if v < minCost
minCost := v
}
return minCost
}
Ovo jednostavno rešenje, na žalost, nije dobro. Koristi mnogo vremena da iznova vrši proračune i njegovo vreme izvršavanja je eksponencijalno.
Koristeći istu adaptaciju kao gore, dobijamo:
function f(m, n) {
if m == n
return 0
else-if f[m,n] != -1:
return f[m,n]
fi
let minCost :=
for k := m to n - 1 {
v := f(m, k) + f(k + 1, n) + c(k)
if v < minCost
minCost := v
}
f[m,n]=minCost
return minCost
}
Parsiranje bilo koje gramatike bez konteksta
[uredi]Specijalni slučajevi gramatika bez konteksta se mogu parsirati mnogo efikasnije nego ovom tehnikom, ali uopšteno, dinamičko programiranje je jedini način.